TRANSFORMADA DE LAPLACE INVERSA Y DE DERIVADAS

May 4, 2022

Apunte

Propiedades de la transformada de Laplace

Sea $f(t)$ una función definida para $t>0$ , si:
$\mathscr{L}[~f(x)~]=F(s) \quad\land\quad \mathscr{L}[~g(x)~]=G(s)$ $\begin{split} \mathscr{L}[~c_1\,f(x)+c_2\,g(x)~]&= c_1\,\mathscr{L}[~f(x)~]+c_2\,\mathscr{L}[~g(x)~]\\ &=c_1\,F(s)+c_2\,G(s) \end{split}$
Si $\mathscr{L}[~f(x)~]=F(s)$ , entonces para alguna constante $a$
$\mathscr{L}[~e^{ax}f(x)~]=F(s-a)$
Si $\mathscr{L}[~f(x)~]=F(s)$ , entonces $\forall \,n\in \Z^+$
$\mathscr{L}[~x^{n}f(x)~]=(-1)^n \,\frac{d^n}{ds^n} \,[~F(s)~]$
Si $\mathscr{L}[~f(x)~]=F(s)$ , y si $\displaystyle\lim_{x\to0} \frac{f(x)}{x}\;:\; x>0$ existe, entonces:
$\mathscr{L}[~\frac{1}{x}\,f(x)~]=\int\limits_{s}^{\infty} F(t)\,dt$
Si $f(x)$ es periódico con periodo $\omega$ , esto es, $f(x+\omega)=f(x)$ , entonces:
$\mathscr{L}[~f(x)~]=\cfrac{\int_{s}^{\infty} e^{-sx}f(x)\, dx}{1-e^{-\omega s}}$

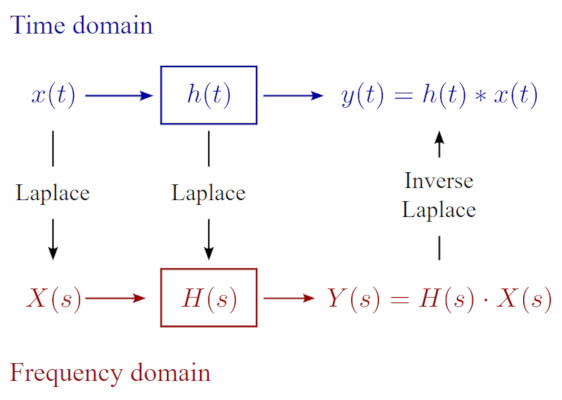
Sea $f(t)$ una función definida para $t>0$ , ademas sabemos la definición de la transformada de Laplace:

\mathscr{L}[f(t)]=F(s) :=\int\limits_{0}^{\infty} e^{-st}\,f(t)\,dt

Entonces la transformada inversa de Laplace:

\mathscr{L}^{-1}[F(s)]=f(t)

\boxed{~~F(s)~~} \qquad\longrightarrow\qquad \boxed{~~f(t)=\mathscr{L}^{-1}[\,F(s)\,]~~}

\frac{1}{s} \qquad\qquad\longrightarrow\qquad\qquad 1

\frac{1}{s^2} \qquad\qquad\longrightarrow\qquad\qquad t

\frac{2!}{s^3} \qquad\qquad\longrightarrow\qquad\qquad t^2

\frac{n!}{s^{n+1}} \qquad\qquad\longrightarrow\qquad\qquad t^n

\frac{1}{s-a} \qquad\qquad\longrightarrow\qquad\qquad e^{at}

\frac{a}{s^2+a^2} \qquad\qquad\longrightarrow\qquad\qquad \sin(at)

\frac{s}{s^2+a^2} \qquad\qquad\longrightarrow\qquad\qquad \cos(at)

\frac{a}{s^2-a^2} \qquad\qquad\longrightarrow\qquad\qquad \sinh(at)

\frac{s}{s^2-a^2} \qquad\qquad\longrightarrow\qquad\qquad \cosh(at)

Si $f'(t)$ es continua cuando $t \geq 0$ , asumiendo que $e^{-st}f(t)\rightarrow 0$ cuando $t\rightarrow\infty$ entonces:

\begin{align*} \mathscr{L}[~f'(t)~]&=\int\limits_{0}^{\infty} e^{-st}\,f'(t)\,dt\\ &=e^{-st}f(t) \Big|_{0}^\infty + s\int\limits_{0}^{\infty} e^{-st}\,f(t)\,dt\\ &=-f(0)+s\,\mathscr{L}[~f(t)~] \end{align*}

Entonces:

\begin{align} \mathscr{L}[~f'(t)~]&=sF(s){\color{magenta}-f(0)} \\ \mathscr{L}[~f''(t)~]&= s^2F(s)-sf(0){\color{magenta}-f'(0)}\\ \mathscr{L}[~f'''(t)~]&=s^3F(s)-s^2f(0)-sf'(0){\color{magenta}-f''(0)}\\ \end{align}

\mathscr{L}[~f^n(t)~] =s^{n}F(s)-s^{n-1}f(0)-s^{n-2}f'(0)-\cdots{\color{magenta}-f^{n-1}(0)}

Sii $f,f',f'',\dots,f^{n-1}$ son continuas en $t\geq0$ y de orden exponencial, y si $f^{n}$ es continua por tramos en $t>0$

Si $\mathscr{L}[~f(t)~]=F(s)$ , entonces:

\mathscr{L}[~t\,f(t)~]=-\frac{d}{ds}\mathscr{L}[~f(t)~]=-\frac{dF}{ds}=-F'(s)

Calcular:
$\mathscr{L}^{-1}\left[ \frac{4s-6}{(s-1)(s-2)(s-3)} \right]$
Utilice fracciones parciales

Solución 🎁

Para:
$\frac{4s-6}{(s-1)(s-2)(s-3)}$
Se tiene:
$\frac{A}{(s-1)}+\frac{B}{(s-2)}+\frac{C}{(s-3)}$
Finalmente:
$\mathscr{L}^{-1}\left[ \frac{4s-6}{(s-1)(s-2)(s-3)} \right] = -e^t-2e^{2t}+3e^{3t}$

Dada:
$\mathscr{L}[~\sin(t)~]=\frac{1}{s^2+1}$
Usar transformada de la derivada para obtener $\mathscr{L}[~\cos(t)~]$

Solución 🎁

Sea:
$f(t)=\cos(t)$
Entonces:
${\color{magenta}f'(t)=-\sin(t)}\quad\land\quad {\color{green}f(0)=1}$
Aplicando la transformada sobre $f'$ :
$\begin{align*} \mathscr{L}[~{\color{magenta}f'(t)}~]&=F'(s)\\ \mathscr{L}[~{\color{magenta}-\sin(t)}~] &= s\,\mathscr{L}[~\cos(t)~]\color{green}-f(0)\\ 1-\mathscr{L}[~\sin(t)~] &=s\,\mathscr{L}[~\cos(t)~] \\ \mathscr{L}[~\cos(t)~] &=\frac{1-\mathscr{L}[~\sin(t)~]}{s}\\ &=\frac{1}{s} \left( 1-\frac{1}{s^2+1} \right)\\ &=\frac{1}{s} \left( \frac{s^2+1-1}{s^2+1} \right)\\ &=\frac{s}{s^2+1} \end{align*}$

Encontrar:
$\mathscr{L}[~t\,\cos(\omega t)~]$
Usar derivada de la transformada

Solución 🎁

Se sabe que:
$\mathscr{L}[~\cos(\omega t)~]=\frac{s}{s^2+\omega^2}$
Entonces:
$\mathscr{L}[~t\,\cos(\omega t)~]=-\frac{d}{ds}\left(\frac{s}{s^2+\omega^2}\right)$
Por regla del cociente:
$\begin{align*} \mathscr{L}[~t\,\cos(\omega t)~]&=-\frac{(s^2+\omega ^2)\left(\frac{d}{ds}s\right)-s\left(\frac{d}{ds}(s^2+\omega ^2)\right)}{\left(s^2+\omega ^2\right)^2}\\ &=\frac{s^2+\omega^2-2s^2}{(s^2+\omega^2)^2}\\ &=\frac{s^2-\omega^2}{(s^2+\omega^2)^2} \end{align*}$